RequestAnimationFrame与贝塞尔曲线

RequestAnimationFrame

我们在浏览器页面上做动画的工作时，曾使用一个计时器，使用setTimeout，每隔多少毫秒进行一次改变来实现动画的效果。
所以浏览器厂家决定, “hey, 为什么我们不提供一个 API 给你, 因为我们可以为你优化一些东西”
因此，这个 API 可以用于动画，无论是改变 DOM 样式，还是 canvas 或 WebGL 的改变。

浏览器可以优化将动画并入为一次单独的 repaint 和 reflow 流程周期，保持动画的高保真。例如，基于JavaScript 的动画与 CSS transitions 或 SVG SMIL 动画 同步.

setTimeout 定时器会在指定的延迟时间过后将回调函数放入回调队列，然后在适当的时候执行。由于 JavaScript 的单线程特性，如果存在其他任务或阻塞操作，setTimeout 的回调函数可能无法按时执行。

requestAnimationFrame 是由浏览器提供的 API，用于在下一次浏览器重绘页面之前执行回调函数，这通常与显示器的刷新频率同步。它会根据浏览器的绘制能力和刷新频率（通常是每秒60帧）来进行调度和优化，避免了过度绘制或不必要的计算，确保动画的流畅性和性能优化。

如果你在浏览器通过requestAnimationFrame运行的动画循环离开这个浏览器标签(tab)时或最小化时， 浏览器不会保持运行动画， 这意味着消耗更少的 CPU, GPU 和内存资源, 还节省电池电量。

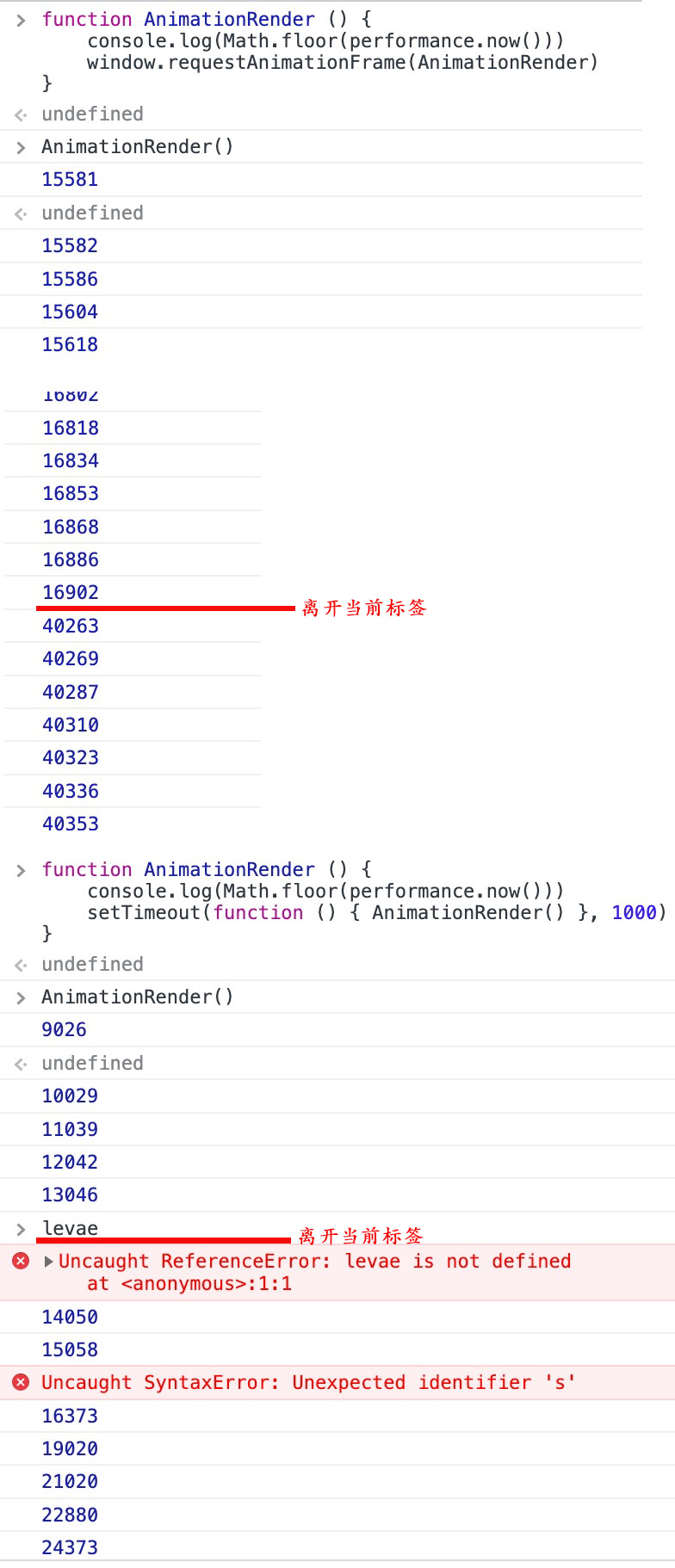
如果当前使用 setTimeout 来驱动动画计时，如下所示：
var handle = setTimeout(renderLoop, PERIOD);

你可以将 setTimeout 替换为 requestAnimationFrame，如下所示
var handle = requestAnimationFrame(renderLoop);

一个Polyfill

for(var x = 0,lastTime = 0,vendors =['ms', 'moz', 'webkit', 'o']; x < vendors.length && !window.requestAnimationFrame; ++x) {
    window.requestAnimationFrame = window[vendors[x]+'RequestAnimationFrame'];
    window.cancelAnimationFrame = window[vendors[x]+'CancelAnimationFrame'] || window[vendors[x]+'CancelRequestAnimationFrame'];
}
window.requestAnimationFrame||(window.requestAnimationFrame=function(callback){
    var currTime = new Date().getTime(),timeToCall = Math.max(0, 16 - (currTime - lastTime)),id = window.setTimeout(function() { callback(currTime + timeToCall); }, timeToCall),lastTime = currTime + timeToCall;return id;
});
window.cancelAnimationFrame||(window.cancelAnimationFrame = function(id) {clearTimeout(id);});

上面 timeToCall 的值会接近16毫秒，这些比较接近 60fps(60 frame per second).

原文:http://paulirish.com/2011/requestanimationframe-for-smart-animating/

绘制贝塞尔曲线

基于贝塞尔曲线的动画可以使用 requestAnimationFrame 结合数学计算来实现平滑的过渡效果。

贝塞尔曲线(Bezier curve)最初由Paul de Casteljau于1959年运用de Casteljau演算法开发，以稳定数值的方法求出贝塞尔曲线。

贝塞尔曲线于1962，由法国工程师皮埃尔·贝塞尔（Pierre Bezier）所广泛发表，他运用贝塞尔曲线来为汽车的主体进行设计。

我们在Photoshop上用到的钢笔工具就是来做这种矢量曲线的。贝塞尔曲线是计算机图形学中相当重要的参数曲线。

一阶贝塞尔（直线）B(t) = p0 + (p1-p0)*t = p0*(1-t) + p1*t (p0为start point, p1为end point)

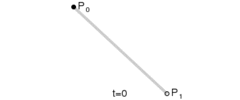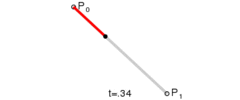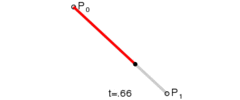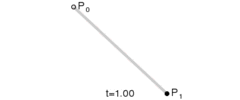
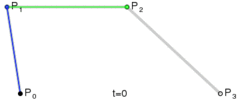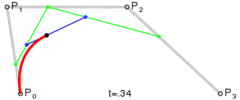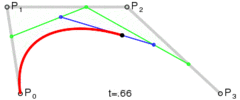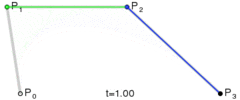
二阶贝塞尔 B(t) = Pm(t)*(1-t) + Pn(t)*t = p0*(1-t)*(1-t) + 2*p1*(1-t)*t+ p2*t*t (p0为start point, p2为end point, p1为control point)

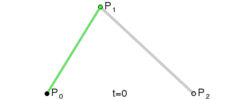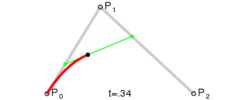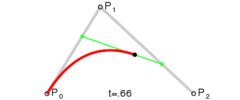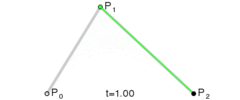
三阶贝塞尔JavaScript:

function c_bezier(p0,p1,p2,p3,t){
    return p0*(1-t)*(1-t)*(1-t)+3*p1*t*(1-t)*(1-t)+3*p2*t*t*(1-t)+p3*t*t*t;
}

四阶

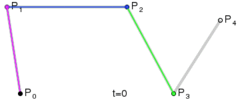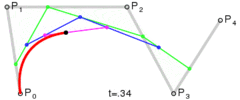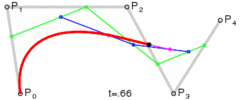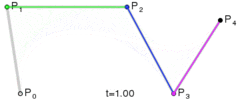
五阶

DEMO

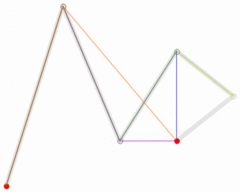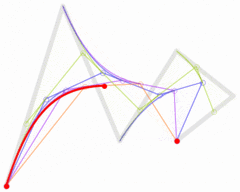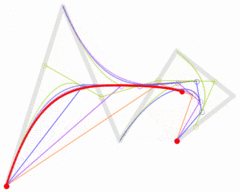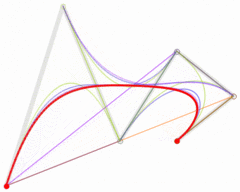
/** usage:*/
var linear = document.getElementById("linear"),
  ease = document.getElementById("ease"),
  ease_in = document.getElementById("ease_in"),
  ease_out = document.getElementById("ease_out"),
  ease_in_out = document.getElementById("ease_in_out"),
  stopped,
  requestId = 0,
  starttime;

function AnimationRender() {
    if (!stopped) {
        var t=((new Date).getTime() - starttime)/1000; // getTime()取得的是毫秒，1s=1000ms
        linear.style.width =c_bezier(0, 0, 1, 1, t)*900 + "px";
        ease.style.width =c_bezier(0.25, 0.1, 0.25, 1, t)*900 + "px";
        ease_in.style.width =c_bezier(0.42, 0, 1, 1, t)*900 + "px";
        ease_out.style.width =c_bezier(0, 0, 0.58, 1, t)*900 + "px";
        ease_in_out.style.width =c_bezier(0.42, 0, 0.58, 1, t)*900 + "px";
        if(t<1) {
            window.requestAnimationFrame(AnimationRender);
        } else {
            AnimationComplete();
            linear.style.width = "900px";
            ease.style.width = "900px";
            ease_in.style.width = "900px";
            ease_out.style.width = "900px";
            ease_in_out.style.width = "900px";
        }
    }
}
/**
 * 贝赛尔曲线 CSS 3:	
 * http://www.w3.org/TR/css3-transitions/#transition-timing-function_tag
 */
function c_bezier(p0,p1,p2,p3,t){
    return p0*(1-t)*(1-t)*(1-t)+3*p1*t*(1-t)*(1-t)+3*p2*t*t*(1-t)+p3*t*t*t;
}
function AnimationStart() {
    starttime = (new Date).getTime();
    requestId =window.requestAnimationFrame(AnimationRender);
    stopped = false;
}
function AnimationComplete() {
    window.cancelAnimationFrame(requestId);
    stopped = true;
}

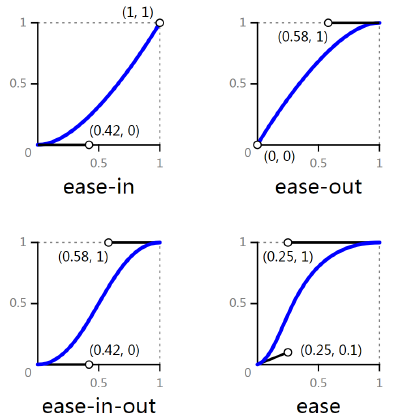
CSS3中transitions中transition-timing-function参数的实现：
ease: Equivalent to cubic-bezier(0.25, 0.1, 0.25, 1).
ease-in: Equivalent to cubic-bezier(0.42, 0, 1, 1).
ease-out: Equivalent to cubic-bezier(0, 0, 0.58, 1).
ease-in-out: Equivalent to cubic-bezier(0.42, 0, 0.58, 1).